Trapez Einfach Erklärt: Definition, Formeln & Übungen!

Haben Sie sich jemals gefragt, warum bestimmte geometrische Formen uns so vertraut erscheinen? Die Antwort liegt oft in ihrer Einfachheit und Vielseitigkeit, wie beim Trapez, einem Viereck, das in überraschend vielen Bereichen unseres Lebens eine Rolle spielt. Ob in der Architektur, im Ingenieurwesen oder sogar in der Kunst, das Trapez begegnet uns ständig, oft unbemerkt.

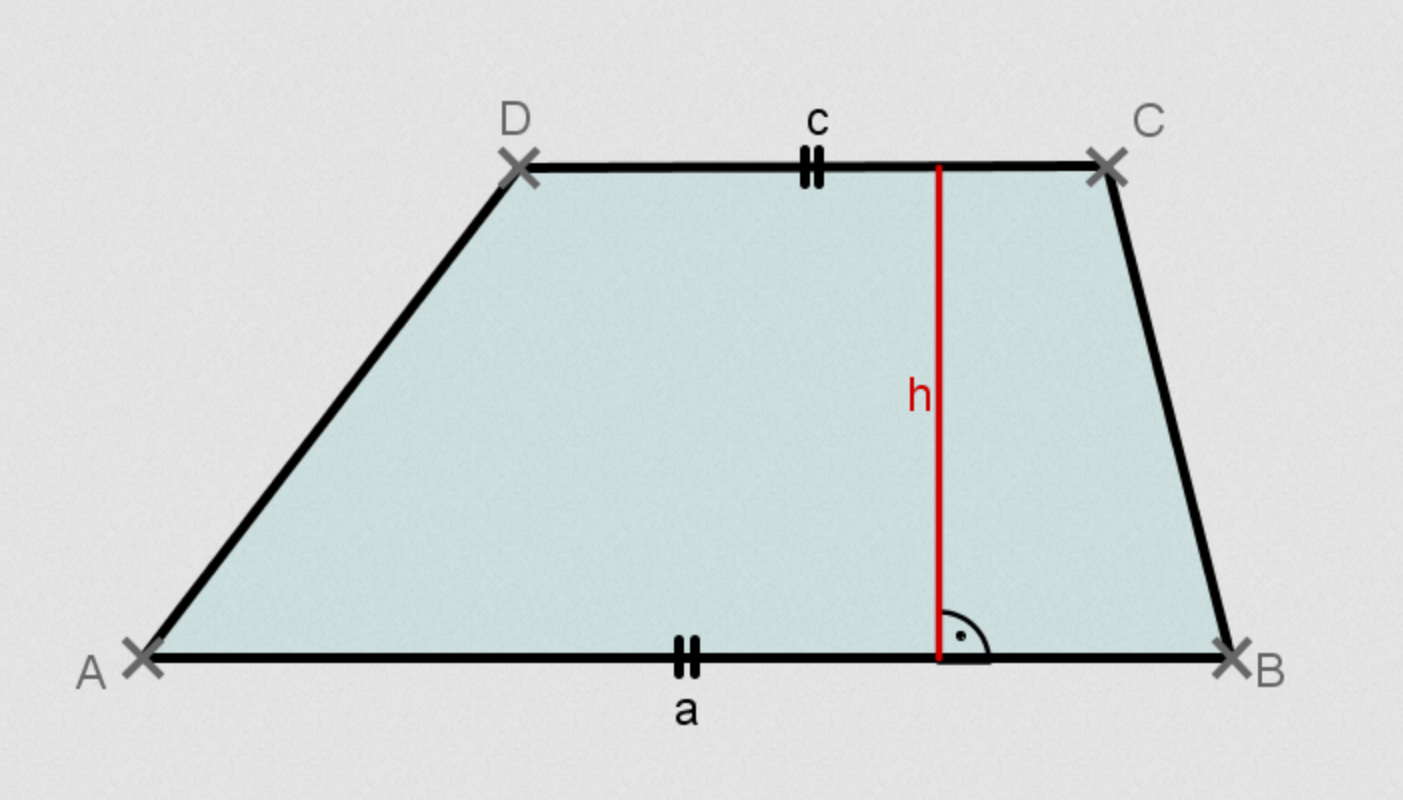
Das Trapez, in der ungarischen Sprache als "trapéz" bezeichnet, ist mehr als nur eine geometrische Figur. Es ist ein faszinierendes Objekt, dessen Eigenschaften und Berechnungen uns einen tieferen Einblick in die Welt der Mathematik ermöglichen. Es ist eine Art von Viereck, und wer sich gerade damit beschäftigt oder sein Wissen auffrischen möchte, findet hier eine nützliche Zusammenfassung. Das Trapez zeichnet sich durch mindestens ein Paar paralleler Seiten aus, was ihm eine besondere Stellung unter den Vierecken verleiht. Diese parallelen Seiten werden als Grundseiten bezeichnet, während die anderen beiden Seiten als Schenkel bezeichnet werden. Die Vielfalt der Trapeze ist groß; es gibt gleichschenklige Trapeze, bei denen die Schenkel gleich lang sind, rechtwinklige Trapeze mit mindestens einem rechten Winkel und allgemeine Trapeze, die keine besonderen Bedingungen erfüllen. Die Berechnung des Flächeninhalts und des Umfangs eines Trapezes ist ein grundlegendes Konzept in der Geometrie und findet in zahlreichen praktischen Anwendungen Verwendung. Die Formel für den Flächeninhalt lautet A = (a + c) / 2 h, wobei a und c die Längen der parallelen Seiten und h die Höhe des Trapezes sind. Der Umfang wird einfach durch die Addition aller vier Seiten berechnet. Das Verständnis dieser Konzepte ist nicht nur für Schüler und Studenten von Bedeutung, sondern auch für Fachleute in verschiedenen Bereichen wie Architektur, Ingenieurwesen und Design. Darüber hinaus bietet das Trapez eine hervorragende Möglichkeit, geometrische Probleme zu lösen und das räumliche Denken zu fördern.

Hier ist eine Tabelle mit einigen verwandten Informationen zum Trapez:

• Neu Lustige Bilder Sprche Kostenlos Zum Teilen
• Hhn Heilbronn Alles Wichtige Zu Studium Terminen Co

Eigenschaft	Beschreibung
Definition	Ein Viereck mit mindestens einem Paar paralleler Seiten.
Grundseiten	Die beiden parallelen Seiten des Trapezes.
Schenkel	Die beiden nicht-parallelen Seiten des Trapezes.
Höhe	Der senkrechte Abstand zwischen den Grundseiten.
Flächeninhalt	A = (a + c) / 2 h, wobei a und c die Längen der Grundseiten und h die Höhe ist.
Umfang	Die Summe aller vier Seiten.
Spezielle Trapeze	Gleichschenkliges Trapez (Schenkel sind gleich lang), rechtwinkliges Trapez (mindestens ein rechter Winkel).
Winkel	Die Winkel an den Grundseiten können unterschiedlich sein, aber die Winkel an jedem Schenkel addieren sich zu 180 Grad.
Symmetrie	Gleichschenklige Trapeze sind achsensymmetrisch.

Für weitere Informationen zum Trapez empfehle ich, die Wikipedia-Seite zum Trapez zu besuchen.

In der türkischen Sprache werden Trapezbleche als "trapez sac" bezeichnet, und ihre Preise variieren je nach verschiedenen Faktoren. Laut der Preisliste von Yapıpan für Trapezbleche im Jahr 2024 beträgt der Preis für ein lackiertes Trapezblech mit einer Dicke von 0,40 mm durchschnittlich 165 TL pro Quadratmeter. Trapezbleche mit einer Dicke von 0,50 mm kosten durchschnittlich 195 TL. Es ist wichtig zu beachten, dass Trapezblechprodukte in einer Mindestgröße von 2 Quadratmetern zugeschnitten und geliefert werden. Diese Informationen sind besonders nützlich für Bauherren und Architekten, die Trapezbleche für ihre Projekte benötigen. Die Preise können je nach Anbieter und Region variieren, daher ist es ratsam, mehrere Angebote einzuholen, um das beste Preis-Leistungs-Verhältnis zu erzielen. Die Qualität des Materials und die Beschichtung spielen ebenfalls eine wichtige Rolle bei der Preisgestaltung. Hochwertige Beschichtungen bieten einen besseren Schutz vor Korrosion und verlängern die Lebensdauer des Trapezblechs. Darüber hinaus können spezielle Anforderungen wie bestimmte Farben oder Zuschnitte den Preis beeinflussen. Es ist auch wichtig, die Lieferkosten und die Montagekosten zu berücksichtigen, um ein vollständiges Bild der Gesamtkosten zu erhalten. Die Wahl des richtigen Trapezblechs hängt von den spezifischen Anforderungen des Projekts ab, einschließlich der Tragfähigkeit, der Witterungsbeständigkeit und des ästhetischen Erscheinungsbilds.

In der polnischen Sprache wird das Trapez als "trapez" bezeichnet. Um die Höhe eines Trapezes zu berechnen, ist es oft notwendig, sich auf die entstandenen Dreiecke zu stützen. Es ist hilfreich, diese Dreiecke separat zu zeichnen, um die Berechnungen zu erleichtern. Die Eigenschaften der Winkel in einem Trapez sind ebenfalls wichtig zu beachten. Die Summe der Winkel Alpha und Delta beträgt 180 Grad, ebenso wie die Summe der Winkel Beta und Gamma. Diese Beziehungen sind entscheidend für die Lösung geometrischer Probleme im Zusammenhang mit Trapezen. Die Kenntnis der Eigenschaften von Trapezen ist nicht nur für Schüler und Studenten von Bedeutung, sondern auch für Ingenieure und Architekten, die diese Formen in ihren Projekten verwenden. Darüber hinaus kann das Verständnis der Winkelbeziehungen in einem Trapez bei der Lösung von komplexeren geometrischen Problemen hilfreich sein. Es ist auch wichtig zu beachten, dass es verschiedene Arten von Trapezen gibt, wie z.B. gleichschenklige Trapeze und rechtwinklige Trapeze, die jeweils spezifische Eigenschaften aufweisen. Die Fähigkeit, diese verschiedenen Arten von Trapezen zu identifizieren und ihre Eigenschaften zu verstehen, ist entscheidend für die erfolgreiche Anwendung geometrischer Konzepte in der Praxis. Darüber hinaus kann die Verwendung von interaktiven Übungen und Simulationen das Verständnis von Trapezen und ihren Eigenschaften weiter verbessern.

• Onlyfans Revolution Oder Risiko Ein Blick Auf Stars Leaks
• Kuchen Ohne Backen Die Besten Rezepte Amp Chefkoch Tipps

Das Trapez ist ein Viereck mit zwei parallelen Seiten. Da an ein Viereck nicht sehr viele Anforderungen gestellt werden, ist es oft schwierig, Berechnungen an ihm durchzuführen. In jedem Trapez sind die Winkel an den nicht-parallelen Seiten supplementär, d.h. ihre Summe beträgt 180 Grad. Dies ist eine wichtige Eigenschaft, die bei der Lösung von geometrischen Problemen im Zusammenhang mit Trapezen hilfreich sein kann. Die Berechnung des Flächeninhalts, des Umfangs, der Winkel, der Schwerpunktsabstände und der Schenkellängen eines Trapezes ist ein grundlegendes Konzept in der Geometrie. Es gibt verschiedene Formeln und Methoden, um diese Berechnungen durchzuführen, und die Wahl der geeigneten Methode hängt von den gegebenen Informationen ab. Darüber hinaus kann die Verwendung von geometrischen Konstruktionen und interaktiven Werkzeugen das Verständnis von Trapezen und ihren Eigenschaften weiter verbessern. Es ist auch wichtig zu beachten, dass es verschiedene Arten von Trapezen gibt, wie z.B. gleichschenklige Trapeze und rechtwinklige Trapeze, die jeweils spezifische Eigenschaften aufweisen. Die Fähigkeit, diese verschiedenen Arten von Trapezen zu identifizieren und ihre Eigenschaften zu verstehen, ist entscheidend für die erfolgreiche Anwendung geometrischer Konzepte in der Praxis. Darüber hinaus kann die Verwendung von realen Beispielen und Anwendungen das Verständnis von Trapezen und ihren Eigenschaften weiter verbessern. Zum Beispiel können Brücken, Dächer und andere architektonische Strukturen oft trapezförmige Elemente enthalten.

Entdecken Sie eine vielseitige Auswahl effektiver Übungen zum gezielten Training Ihres Trapezmuskels. Trapezübungen können jetzt online mit Schülerhilfe gelernt werden, um durchzustarten und Noten zu verbessern. Die Konstruktion des Schwerpunkts im Trapez und auch der Übergang vom Trapez zum Dreieck kann im folgenden Applet nachvollzogen werden. Applet laden von GeoGebra mit einem Klick auf Bild oder Button oben stimmen Sie zu, dass externe Inhalte von GeoGebra geladen werden. Der Trapezmuskel, auch bekannt als Kapuzenmuskel, ist ein großer Muskel, der sich vom Hinterkopf bis zu den Schultern und dem mittleren Rücken erstreckt. Er spielt eine wichtige Rolle bei der Bewegung und Stabilität des Kopfes, des Halses und der Schultern. Ein gezieltes Training des Trapezmuskels kann die Körperhaltung verbessern, Schulterschmerzen reduzieren und die allgemeine Muskelkraft erhöhen. Es gibt verschiedene Übungen, die den Trapezmuskel trainieren können, wie z.B. Schulterheben, Rudern und Gesichtszüge. Die Wahl der geeigneten Übung hängt von den individuellen Bedürfnissen und Zielen ab. Es ist wichtig, die Übungen korrekt auszuführen, um Verletzungen zu vermeiden und die bestmöglichen Ergebnisse zu erzielen. Darüber hinaus kann die Verwendung von Gewichten und Widerstandsbändern die Intensität der Übungen erhöhen und die Muskelkraft weiter verbessern. Es ist auch wichtig, den Trapezmuskel regelmäßig zu dehnen, um Verspannungen zu lösen und die Flexibilität zu erhöhen.

Flächeninhalt und Umfang » Trapez Der Flächeninhalt und der Umfang des Trapezes. Das Trapez ist ein Viereck, dessen zwei Seiten parallel sind. Die parallelen Seiten nennen wir Basen und die anderen Säulen. Das Trapez wird zuerst verdoppelt, dann wird das zweite Trapez um 180° gedreht an das erste angefügt. Wir erhalten ein Parallelogramm, das den doppelten Flächeninhalt des Trapezes hat. Deshalb wird in der Formel (a + c) durch 2 geteilt. Im Lateinischen bedeutet trapezius, man mag es vermutet haben, trapezförmig. Es gibt weitere Bezeichnungen für den Trapezmuskel, so etwa Kappenmuskel oder auch Kapuzenmuskel. Bezeichnend ist der Name Trapezmuskekl übrigens schlicht, weil die beiden dreieckigen Einzelmuskeln gemeinsam ein Art Viereck oder eben weitläufiger ein Trapez bilden. Entdecke eine vielseitige Auswahl effektiver Übungen zum gezielten Training deines Trapezmuskels. Trapezturnen erfordert einen gute Körperkontrolle. Trainerin Gina Laskowski zeigt in dieser Folge #fitwoch, wie aus einfachen Übungen eine kreative Choreogra Jede Übung ist verständlich mit Text, Bild und Animationen erklärt. Für Lehrkräfte & Schülerinnen digitale Produkte jetzt entdecken! Trapez i interaktive Übung auf oebv.at: Für Lehrkräfte & Schülerinnen digitale Produkte jetzt entdecken!

Ein Trapez ist ein solches Viereck, das ein paralleles Seitenpaar hat. Seine Fläche und sein Umfang lassen sich auch leicht berechnen, mit Hilfe der Seiten und der Höhe. Das Trapez lässt sich wie alle Vierecke auch in das sogenannte Haus der Vierecke einordnen. Im folgenden Bild ist das Trapez in Orange in der zweiten Etage von unten zu sehen. Das Haus der Vierecke ordnet die darin enthaltenen Vierecke nach ihren Eigenschaften ein. Ganz unten steht das allgemeine Viereck, dem keine speziellen Eigenschaften das Trapez sac lässt sich wie alle Vierecke auch in das sogenannte Haus der Vierecke einordnen.

Das Trapez, ungarisch "trapéz", definiert durch seine parallelen Seiten und vielfältigen Anwendungsmöglichkeiten, ist ein zentrales Element der Geometrie. Seine Definition, Eigenschaften, Umfang- und Flächenberechnung sowie spezielle Formen und zugehörige Aufgaben bieten ein breites Spektrum an Lern- und Anwendungsmöglichkeiten. Ob in der ungarischen Terminologie oder in anderen Sprachen, das Verständnis des Trapezes eröffnet neue Perspektiven in der Welt der Mathematik und ihrer praktischen Anwendungen.

Das Trapez ist ein Viereck, in dem zwei gegenüberliegende Seiten a, b parallel sind. Die restlichen zwei Seiten c, d nennen wir Arme des Trapezes.

Hier ist eine Tabelle mit Informationen zu den Preisen von Trapezblechen (Trapez sac) in der Türkei, basierend auf Daten von 2024:

Eigenschaft	Beschreibung
Material	Trapezblech (Trapez sac)
Preisbasis	Preise in türkischer Lira (TL)
Messung	Preise pro Quadratmeter (m²)
Hersteller	Yapıpan (basierend auf der Liste von 2024)
Dicke	0.40 mm
Beschichtung	Lackiert
Durchschnittlicher Preis pro m²	165 TL
Dicke	0.50 mm
Durchschnittlicher Preis pro m²	195 TL
Mindestabnahme	Die Produkte werden in einer Mindestgröße von 2 m² geschnitten und geliefert.

Für weitere Informationen zu Trapezblechen und deren Preisen in der Türkei können Sie die Website von Yapıpan besuchen.

• Candii Kayn Gewichtszunahme Kemono Amp Onlyfans Was Steckt Dahinter
• Katelyn Elizabeth Nackt Die Heiesten Leaks Videos

Details

Aufgaben zum Trapez

Details

Gleichschenkliges Trapez • Eigenschaften · [mit Video]

Details

Gleichschenkliges Trapez • Eigenschaften · [mit Video]